Proportional Reasoning - Proportional Sets
Gain an overview of the concepts and relationships that underpin a secure understanding of proportional sets including generating proportional sets of numbers, recognising the relationships that make two sets of numbers proportional, and applying proportional sets to contexts. Consider the language and notation that will extend pupils’ thinking. Support this with images that will stimulate dialogue about proportional reasoning.In addition to this essential summary you will find links to further ideas for the classroom.
What are the fundamental concepts and relationships?
- Generating proportional sets of numbers by:
- starting from a pair of numbers, apply the same multiplier to each to create another pair of numbers in the same ratio; repeat the process with any multiplier. For example, application to tables of conversions.
- Recognising the relationships that make two sets of numbers proportional by:
- checking for equality of ratios between corresponding pairs of numbers, or
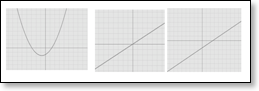
- establishing whether the relationship is a linear one, and then whether the line passes through the origin.
- Application of proportional sets to the context of:
- geometry, such as similarity, enlargement, and trigonometry
- number and algebra, such as constant rates of change, (for example, gradient, speed, and growth).
What is the associated language and notation?
These notations and their associated language describe the relationships and equivalences that pupils need to understand and use:
- Using the term ‘proportional’ to describe relationships. For example, the circumference of a circle is proportional to its diameter.
- Comparing quantities that are parts of a whole. For example, these facts will generate proportional sets: 1 ‘in every’ 10 children does not eat breakfast, 5 ‘out of every’ 10 dogs dream.
- Tabular representation of proportional sets. For example, coordinates of points on a straight line passing through the origin.
- Algebraic representation of a proportional relationship between two variables, y and x: y = kx, where k is a constant.
- Using the term ‘rate’ to describe proportional relationships. For example, currency exchange rates, conversion rates from metric to Imperial measures.
Find more support and further examples in Proportional sets mental activities.
These activities focus on the comparison of quantities, giving pupils opportunities to become more fluent in
- generating proportional sets of numbers
- checking sets of numbers for proportionality
- exploring contexts for proportional sets
- making connections between ratios and proportional sets of numbers, and rates and proportional sets of numbers.
Teaching resources for proportional sets images
Find tried and tested classroom resources in Proportional Sets - Making Connections.
What are appropriate supporting images?
Graphs of proportional sets of numbers and comparison with other linear and non-linear functions
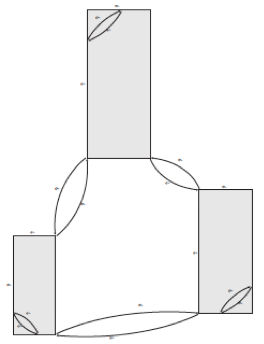
Use images of geometric shapes, including right-angled triangles, to identify ‘within’ and ‘between’ aspects of dimensions, applying ratio and scaling to explore similarity.
Photographic enlargements
Shadows
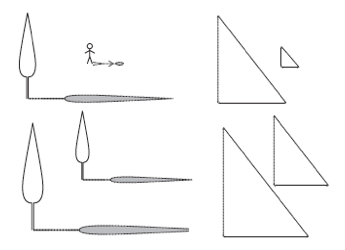
These can be used to:
- generate proportional sets of numbers related to a context
- apply proportional sets to geometry
- develop understanding of graphical representation of proportional relationships.