Proportional Reasoning: Scaling
Gain an overview of the concepts and relationships that underpin a secure understanding of scaling including identification of the multiplying factor and its inverse and making connections between single operator scaling and unitary methods.
- Consider the language and notation that will extend pupils’ thinking.
- Support this with images that will stimulate dialogue about proportional reasoning.
What are the fundamental concepts and relationships?
- Identifying multipliers/scale factors.
- Establishing a single multiplier between any two numbers and identifying the inverse multiplier.
- The importance of identifying what constitutes the ‘original’ and hence the scaling operation (including the single multiplier) required.
- Making connections between single operator scaling and unitary methods.
- Using ratio and scaling to explore similarity comparing:
- corresponding dimensions between shapes.
What is a Fraction? is a short booklet which provides further detail on these concepts and relationships.
What is the associated language and notation?
- These notations and their associated language describe the relationships and equivalences that pupils need to understand and use:
- Using the fact that dividing by a number is equivalent to multiplying by its reciprocal
- Using reciprocals as multiplicative inverses, that is multiplying by 1/3 is the inverse of multiplying by 3
- Multiplying by 7/3 is equivalent to multiplying by 1/3 (or dividing by 3) and multiplying by 7
- Understanding that 7/3 is the scaling factor from one quantity to the other when the ratio of the quantities is 7:3. (‘Seven thirds of’ is the relative size of one quantity compared with the other when the ratio of the quantities is 7:3).
- Equivalence of operators, for example,
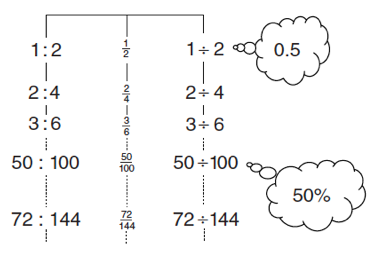
Find more support and further examples in Scaling and enlargement mental activities.
These activities focus on the comparison of quantities, giving pupils opportunities to become more fluent in
• linking together language and notation of scaling
• exploring contexts for scaling
• explaining the effect of using different sizes of multiplier for scaling
• making connections between multipliers expressed as fractions, decimals or percentages.
What are appropriate supporting images?
Develop pupils’ thinking about scaling by establishing a single multiplier between any two numbers using the image of graduated line segments:
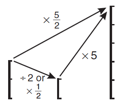
Develop pupils’ understanding of a single multiplier between any two numbers without the need to record an interim step using the image of line segments:
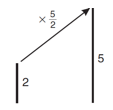
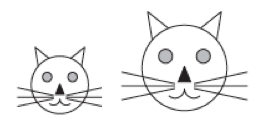
Develop pupils’ thinking about scalings associated with enlargement of 2D shapes using the following images.
Cat faces
Photographic enlargements
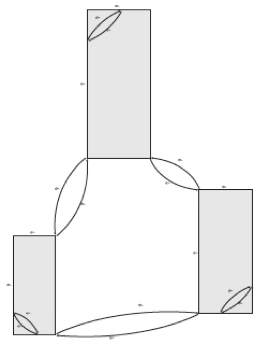
Shadows
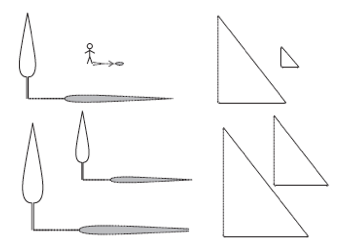
These can be used to identify ‘within’ and ‘between’ aspects of dimensions of similar shapes. Using ratio and scaling to explore similarity comparing:
- internal dimensions of a shape
- corresponding dimensions between shapes.