Proportional Reasoning - Fractions
Gain an overview of the concepts and relationships that underpin a secure understanding of fractions as both numbers and operators. Consider the language and notation that will extend pupils’ thinking. Support this with images that will stimulate dialogue about proportional reasoning.In addition to this essential summary you will find links to further ideas for the classroom.
What are the fundamental concepts and relationships?
- Fractions as numbers (positions on a number line), that is multiples of unit fractions:
- proper fractions
- improper fractions
- The importance of identifying what constitutes ‘the whole’, i.e. what object or quantity is being divided
- Fractions as multiplicative operators:
- unit fractions, e.g. 1/3 of
- proper fractions, e.g.2/3 of
- improper fractions, e.g. 7/3 of
What is a fraction? is a short booklet which provides further detail on these concepts and relationships.
What is the associated language and notation?
This is a representation of the relationships and equivalences that pupils need to understand and use:
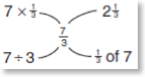
[Note: To be mathematically accurate 3 × 7 is read as ‘3 multiplied by 7’ and means ‘7 lots of 3’. However in these resources we use the conventional language of 3 × 7 as ‘three sevens’.]
Develop language clarifying the object or quantity which is being divided.
E.g. half of the chocolate bar; half of the 6 chocolate bars.
Help pupils to reinforce their understanding and develop confidence with the language of fractions by saying aloud sequences of fractions as in multiplication tables:
- fraction sequences (1,2,3…multiples of the same unit fraction) e.g. 1 × 1/7 , 2 × 1/7 etc
- fraction sequences created using fractions as operators (the same fraction of 1, 2, 3 …) e.g.1/11 of 1, 1/11 of 2, 1/11 of 3 etc.
Extend the language of fractions by using equivalences:
for example, including building the language of mixed numbers through sequences,
e.g.
![]()
Use appropriate images alongside the language. For example, refer to jumps on a number line as an image to link with multiples of a unit fraction.
Find more support and further examples in Fractions mental activities.
What are appropriate supporting images?
Many pupils can offer images to explain their understanding of:
- the part/whole aspect of fractions, e.g. as parts of a chocolate bar
- fractions as numbers, e.g. on number lines :

Develop pupils’ thinking by using of the image of fraction stacks. Taking a row to representing 1, the examples below shows images of 7. The first image is shaded to show ‘one third of seven’ and the second to show ‘seven lots of one third’. The aim is to help pupils see that the shaded parts are equal.![]()
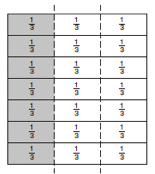
![]()
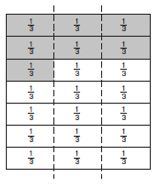
The diagram illustrates the commutative nature of fraction multiplication, i.e.
1/3 × 7 = 7 × 1/3
1/3 of 7 = 7 lots of 1/3
This will enable pupils to reason proportionally by
- convincing them that multiplication is commutative when fractions are involved
- increasing their flexibility in calculation.
Teaching resources for the fraction stacks image
Find tried and tested classroom resources in Using the fraction stacks image.