Proportional Reasoning - Ratio
Gain an overview of the concepts and relationships that underpin a secure understanding of ratio both as a way of comparing quantities that are parts of a whole and of comparing different quantities. Consider the language and notation that will extend pupils’ thinking. Support this with images that will stimulate dialogue about proportional reasoning.
In addition to this essential summary you will find links to further ideas for the classroom.
What are the fundamental concepts and relationships?
- Ratio as a way of comparing quantities:
- parts of a single quantity, e.g. mixing paint
- one quantity with another quantity, e.g. real life distance and distance on a map.
- The importance of identifying what quantity is the basis for comparison.
- Ratios, fractions, decimals and percentages as equivalent ways of comparing.
What is a fraction? is a short booklet which provides further detail on these concepts and relationships.
What is the associated language and notation?
When ratio is used to compare quantities that are parts of a whole, we are also describing proportions. Some connected phrases are: ‘in every’ and ‘out of every’
e.g. 1 ‘in every’ 10 children does not eat breakfast;
5 ‘out of every’ 10 dogs dream
When ratio is used to compare one quantity with another, some connected phrases are: ‘to every’ or ‘for every’ or ‘as many as’
e.g. the scale drawing shows 1cm ‘to every’ 50cm
‘for every’ 2 bags of crisps you get one sticker,
or
there are twice ‘as many’ bags of crisps ‘as’ stickers.
These notations and their associated language describe the relationships and equivalences that pupils need to understand and use:
- The ratio of 7 to 3 equals 7:3
- The inverse ratio of 7 to 3 is 3 to 7 which equals 3:7
- 7:3 and 7/3 are equivalent notations for comparing two quantities. 7/3 (‘seven thirds of’) is the relative size of one quantity compared with the other when the ratio of the quantities is 7:3
- 7/3 is the scaling factor from one quantity to the other when the ratio of the quantities is 7:3
Equivalence of operators, for example,
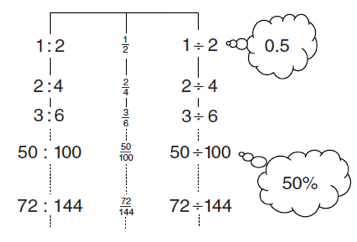
Find more support and further examples in Ratio mental activities.
These activities focus on the comparison of quantities, giving pupils opportunities to become more fluent in
- linking together language and notation of ratio
- exploring contexts for equivalent ratios
- explaining the connections between ratios and fractions .
Many pupils will have an understanding of ratio as a way of making comparisons between the parts that make up a single quantity,
e.g. diluting squash, sharing out a bill for a meal.
Develop pupils’ thinking about ratio as a comparison of one quantity with another by using the image of ratio strips.

- no. of black blocks : no. of white blocks = 2:5
- no. of white blocks : no. of black blocks = 5:2
- no. of black = 2/5 × no. of white, no. of white = 5/2 × no. of black
- no. of black = 0.4 × no. of white, no. of white = 2.5 × no. of black
- no. of black = 40% of no. of white, no. of white = 250% of no. of black
Using this image will help develop pupils’ appreciation of ratio as a way of comparing one quantity with another. This underpins many big ideas in secondary mathematics, e.g. scales on maps and drawings, rates, percentages, enlargement, trigonometry.
Teaching resources for the ratio strips image
Find tried and tested classroom resources in Making Connections.